- Today
- Total
개발하는 고라니
[알고리즘] 플로이드-와샬 (Floyd-Warshall) 본문
그래프가 주어졌을 때 하나의 시작 정점에서 다른 모든 정점들로 가는 최단 경로를 구하는 알고리즘은 다익스트라(Dijkstra)와 벨만-포드(Bellman-Ford)가 있다.
만약 그래프에 존재하는 모든 정점 사이의 최단 경로를 구하려면 다익스트라 알고리즘을 정점의 수(n) 만큼 반복 실행하면 된다. 즉 구해야할 최단 경로가 총 n^2개다. (자기 자신으로의 경로 포함)
하지만 이보다 간단한 방법으로 모든 정점 쌍 사이의 최단 경로를 구하는 방법인 플로이드-와샬(Floyd-Warshall) 알고리즘을 알아보고자 한다. 다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택했다면, 플로이드 와샬 알고리즘은 기본적으로 거쳐가는 정점을 기준으로 알고리즘을 수행한다는 점에서 그 특징이 있다. 또한 이 알고리즘은 동적 프로그래밍 기술에 의거한다. (다익스트라는 음의 가중치를 가진 간선은 사용하지 못하나, 플로이드 와샬은 가능하다)
플로이드 와샬은 Optimal Substructure의 개념을 이용하여 최단 경로를 찾는데, Optimal Substructure이란 특정 경로안에 무수히 많은 경로가 있을 때, 중간 정점들이 각각 최단이 된다면 이를 모두 이은 경로 또한 최단이 된다는 개념이다.
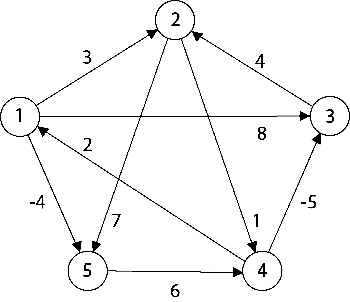
위와 같은 그래프가 있다고 할 때, 초기 표는 다음과 같다.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 3 | 8 | INF | -4 |
| 2 | INF | 0 | INF | 1 | 7 |
| 3 | INF | 4 | 0 | INF | INF |
| 4 | 2 | INF | -5 | 0 | INF |
| 5 | INF | INF | INF | 6 | 0 |
# 모든 정점들이 정점 1을 거쳐갈 때
1에서 1을 거쳐갈 때
자기 자신이므로 해당 (X)
> 2에서 1을 거쳐갈 때
2 -> 1 INF 이므로 (X)
> 3에서 1을 거쳐갈 때
3 -> 1 INF 이므로 (X)
> 4에서 1을 거쳐갈 때
4 -> 2 VS 4 -> 1 -> 2
(INF) > (2 + 3)
∴ 4 -> 2 = 5
> 5에서 1을 거쳐갈 때
5 -> 1 INF 이므로 (X)
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 3 | 8 | INF | -4 |
| 2 | INF | 0 | INF | 1 | 7 |
| 3 | INF | 4 | 0 | INF | INF |
| 4 | 2 | 5 | -5 | 0 | -2 |
| 5 | INF | INF | INF | 6 | 0 |
# 모든 정점들이 정점 2을 거쳐갈 때
1에서 2을 거쳐갈 때
1 -> 4 VS 1 -> 2 -> 4
(INF) > (3 + 1)
∴ 1 -> 4 = 4
> 2에서 2을 거쳐갈 때
자기 자신이므로 (X)
> 3에서 2을 거쳐갈 때
3 -> 4 VS 3 -> 2 -> 4
(INF) > (4 + 1)
∴ 3 -> 4 = 5
3 -> 5 VS 3 -> 2 -> 5
(INF) > (4 + 7)
∴3 -> 5 = 11
> 4에서 2을 거쳐갈 때
4 -> 5 VS 4 -> 2 -> 5
(-2) < (5 + 7)
∴4 -> 5 = -2 그대로 유지
> 5에서 2을 거쳐갈 때
5 -> 2 INF 이므로 (X)
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 3 | 8 | 4 | -4 |
| 2 | INF | 0 | INF | 1 | 7 |
| 3 | INF | 4 | 0 | 5 | 11 |
| 4 | 2 | 5 | -5 | 0 | -2 |
| 5 | INF | INF | INF | 6 | 0 |
# 모든 정점들이 정점 3을 거쳐갈 때
> 1에서 3을 거쳐갈 때
1 -> 2 VS 1 -> 3 -> 2
(3) < (8 + 4)
∴그대로 유지
> 2에서 3을 거쳐갈 때
2 -> 3 INF 이므로 (X)
> 3에서 3을 거쳐갈 때
자기 자신이므로 (X)
> 4에서 3을 거쳐갈 때
4 -> 2 VS 4 -> 3 -> 2
(INF) > (-5 + 4)
∴4 -> 2 = -1
> 5에서 3을 거쳐갈 때
5 -> 3 INF 이므로 (X)
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 3 | 8 | 4 | -4 |
| 2 | INF | 0 | INF | 1 | 7 |
| 3 | INF | 4 | 0 | 5 | 11 |
| 4 | 2 | -1 | -5 | 0 | -2 |
| 5 | INF | INF | INF | 6 | 0 |
위와 같은 방식으로 표를 채워나가면 모든 정점에서의 최단 거리를 구할 수 있다.
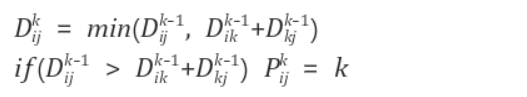
플로이드 와샬 알고리즘의 시간 복잡도는 O(n^3)이다. 다익스트라 알고리즘의 시간 복잡도가 O(n^2) 이므로, n개의 정점에 대하여 다익스트라를 수행하면 O(n^3)이 된다. 즉 플로이드-와샬과 n회 수행하는 다익스트라 알고리즘의 시간 복잡도는 동일하다. 하지만 모든 정점에서의 최단 경로를 구하는 것이 요구된다면, 플로이드 와샬 알고리즘을 사용하는 것이 훨씬 간단하게 작동할 수 있다.
# 완성된 최단경로 표
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | -3 | 2 | -4 |
| 2 | 3 | 0 | -4 | 1 | -1 |
| 3 | 7 | 4 | 0 | 5 | 3 |
| 4 | 2 | -1 | -5 | 0 | -2 |
| 5 | 8 | 5 | 1 | 6 | 0 |
# Code </>
public class FloydWarshall {
static final int INF = 1000000000;
static int n = 5;
static int[][] distance = {
{0, 3, 8, INF, -4},
{INF, 0, INF, 1, 7},
{INF, 4, 0, INF, INF},
{2, INF, -5, 0, INF},
{INF, INF, INF, 6, 0}
};
static void FloydWarshall(){
int[][] d = distance;
for(int k=0; k<n; k++) //k : 거쳐가는 정점
for(int i=0; i<n; i++) //i : 출발 정점
for(int j=0; j<n; j++) //j : 도착 정점
d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
for(int i=0; i<n; i++){
for(int j=0; j<n; j++)
System.out.printf("%2d ", d[i][j]);
System.out.println();
}
}
public static void main(String[] args) {
FloydWarshall();
}
}
# 플로이드 와샬 문제
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
1613번: 역사
첫째 줄에 첫 줄에 사건의 개수 n(400 이하의 자연수)과 알고 있는 사건의 전후 관계의 개수 k(50,000 이하의 자연수)가 주어진다. 다음 k줄에는 전후 관계를 알고 있는 두 사건의 번호가 주어진다.
www.acmicpc.net
11403번: 경로 찾기
가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.
www.acmicpc.net
# References
쉽게 배우는 알고리즘(개정판).문병로.한빛 아카데미
C언어로 쉽게 풀어쓴 자료구조(개정3판).천인국 외3인.생능출판
'Programming > 알고리즘' 카테고리의 다른 글
| [알고리즘] 비트 마스킹(Bit Masking) (0) | 2021.02.21 |
|---|---|
| [알고리즘] Dijkstra 알고리즘 - PriorityQueue (0) | 2021.01.28 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2021.01.28 |
| [알고리즘] 크루스칼(Kruskal) 알고리즘 (0) | 2021.01.28 |
| [알고리즘] 선택 / 버블 / 삽입 정렬 (0) | 2021.01.26 |




