- Today
- Total
개발하는 고라니
[알고리즘] 다익스트라(Dijkstra) 알고리즘 본문
최단 경로
최단 경로 문제에서 입력 그래프의 유형은 크게 두 가지이다.
- 모든 간선 가중치가 음이 아닌 경우
- 음의 가중치가 존재하는 경우
음의 가중치를 허용하지 않는 경우 다익스트라(Dijkstra) 알고리즘으로 이 유형의 문제를 푼다.
음의 가중치를 허용하는 경우 벨만-포드 알고리즘으로 이 유형의 문제를 푼다.
음의 가중치는 허용하지만 가중치 합이 음수인 사이클은 절대 허용하지 않는다. 음의 사이클이 있으면 해당 사이클을 몇번이고 돌아 경로의 가중치 합을 무한정 낮출 수 있기 때문에 최단 경로 문제 자체가 성립하지 않는다.
Dijkstra 알고리즘
다익스트라 알고리즘은 하나의 시작 정점에서 다른 모든 정점까지 최단 경로를 구한다. 다만 이 때 음의 가중치를 갖는 간선은 허용하지 않는다. 임의의 두 정점 간 경로가 존재하지 않으면 이 경로의 길이는 INF(∞)로 정의한다. 또 두 정점 사이에 간선이 없으면 가중치가 INF인 간선이 있다고 간주한다.
이 알고리즘은 동적 프로그래밍(Dynamic Programming, DP)를 활용한 대표적인 최단 경로(Shortest Path)탐색 알고리즘이다. 흔히 인공위성 GPS 소프트웨어 등에서 가장 많이 사용된다. 음의 가중치가 허용되지 않기에 현실 세계에서 사용하기 매우 적합한 알고리즘 중 하나이다.
다익스트라가 DP인 이유는 '최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문이다.' 작은 문제가 큰 문제의 부분 집합에 속해있다고 볼 수 있다. 기본적으로 다익스트라는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있다.
시작 정점인 0에서 다익스트라 알고리즘을 사용해 모든 정점까지의 최단 경로를 구하는 과정을 보자. 프로세스는 다음과 같다.
- 시작 정점을 설정한다.
- 시작 정점을 기준으로 각 정점까지의 최소 비용을 저장한다.
- 방문하지 않은 정점 중 가장 비용이 적은 정점을 선택한다.
- 해당 정점을 거쳐 다른 정점으로 가는 경우를 고려해 최소 비용을 변경한다.
- 3 -> 4번을 반복한다.
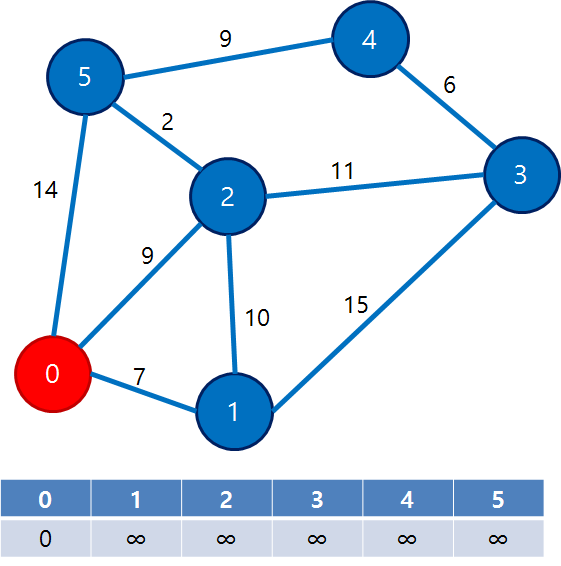
start) 정점 0에서 모든 정점까지의 경로를 INF로 놓는다.

1) 정점 0을 방문했다고 하고, 정점 0과 인접한 정점1, 2, 5에 대한 비용을 distance[]에 갱신한다.
distance = {0, 7, 9, INF, INF, 14}
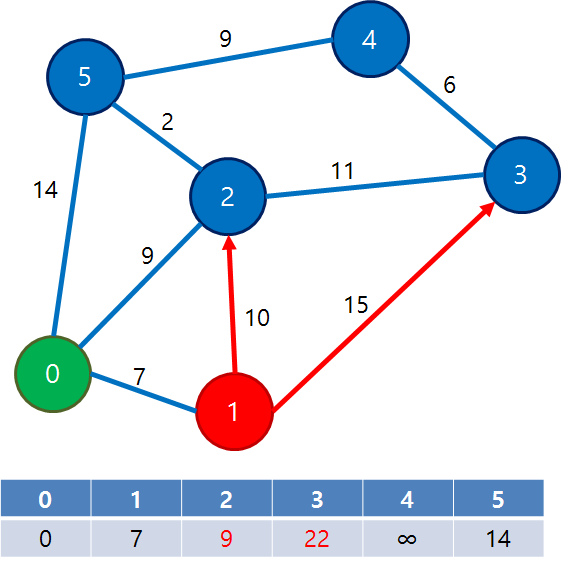
2) distance[] 중 가장 작은 값(7)을 갖고 방문하지 않은 정점은 1번 정점이다.
정점 1을 방문한다.
정점 0에서 1을 통해 갈 수 있는 정점이 있으면 최소 비용(distance[])를 갱신한다.
distance[2] = min(distance[2], distance[1] + 10) = 9
distance[3] = min(distance[3], distance[1] + 15) = 22
distance = {0, 7, 9, 22, INF, 14}
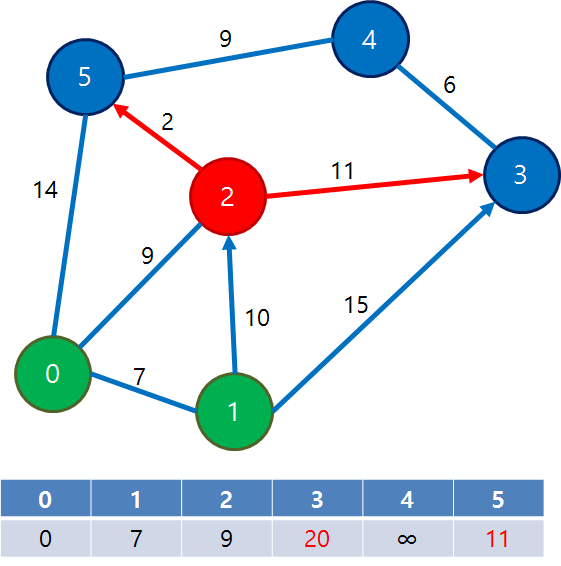
3) distance[] 중 가장 작은 값을 갖고 방문하지 않은 정점은 정점 2이다.
정점 2를 방문한다.
정점 0에서 2를 통하여 갈 수 있는 정점이 있으면 최소 비용을 갱신한다.
distance[5] = min(distance[5], distance[2] + 2) = 11
distance[3] = min(distance[3], distance[2] + 11) = 20
distance = {0, 7, 9, 20, INF, 11}
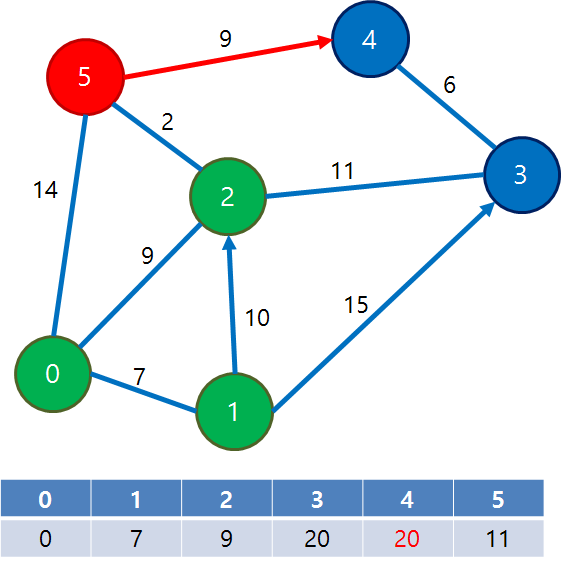
4) distance[] 중 가장 작은 값을 갖고 방문하지 않은 정점은 정점 5이다.
정점 5를 방문한다.
정점 0에서 5를 통하여 갈 수 있는 정점이 있으면 최소 비용을 갱신한다.
distance[4] = min(distance[4], distance[5] + 9) = 20
distance = {0, 7, 9, 20, 20, 11}

5) distance[] 중 가장 작은 값을 갖고 방문하지 않은 정점은 정점 3, 4이다.
정점 3를 방문한다.
정점 0에서 3을 통하여 갈 수 있는 정점이 있으면 최소 비용을 갱신한다.
distance[4] = min(distance[4], distance[3] + 6) = 20
distance = {0, 7, 9, 20, 20, 11}
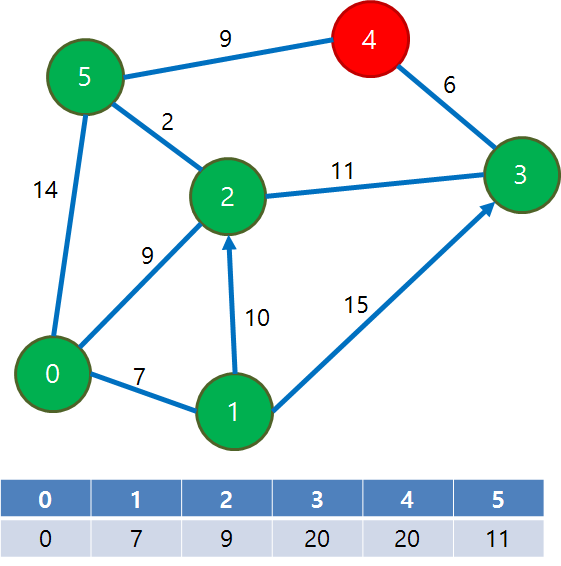
6) distance[] 중 가장 작은 값을 갖고 방문하지 않은 정점은 정점 4이다.
정점 4를 방문한다.
정점 0에서 4를 통하여 갈 수 있는 정점이 없으므로(이미 다 방문해서) 패스
distance = {0, 7, 9, 20, 20, 11}
사진 출처 : Ries 마법의 슈퍼마리오님의 블로그
마지막으로 4번 정점만 남았을 때는 나머지 정점을 다 방문한 상태이므로 아무것도 하지 않는다.
여기까지가 다익스트라 알고리즘 작동의 과정인데, 이게 끝나고 나면 각 distance 값이 0번 정점으로부터의 실제 최단 거리가 된다. 즉 매 루프에서 방문된 상태의 정점의 distance값은 이미 최단거리고, 앞으로 절대 안 바뀐다는 말이다.
만약 이렇게 했는데 최단거리가 구해지지 않는 경우도 있을까?
아직 방문하지 않은 정점들 중 가장 distance 값이 작은 정점이 u고, 사실 distance[u]는 최단거리보다는 아직 크다고 가정하면, 이 때 u를 방문하면 distance[u] 값은 최단거리가 아니게 된다.
또한 distance[u]가 아직 최단거리가 아니라는 말은, 다른 임의의 정점 v를 거치는 경로를 통해 최단거리로 갱신될 수 있다는 말이다. 즉 distance[u] > distance[v] + d[v][u]인 어떤 정점 v가 존재할 것 이다.
그런데 아직 방문하지 않은 정점 중에서 distance 값이 제일 작은 게 u라고 했으니까 v는 방문한 상태일 것 이다.
그런데 v를 방문했을 때 distance[u]는 이미 distance[v] + d[v][u]로 갱신되었을 것이다.
따라서 저렇게 될 수 있는 경우는 없다.
# Code </>
public class DijkstraExp {
static final int INF = 1000000000;
static int n = 6;
static boolean[] visit = new boolean[n];
static int[] distance = new int[n];
//가장 최소 거리를 가지는 정점을 반환
static int getMinIdx(){
int min = INF;
int idx = 0;
for(int i=0; i<n; i++)
if(!visit[i] && distance[i] < min){ //방문하지 않았고, 거리가 가장 짧은 곳의 idx
min = distance[i];
idx = i;
}
return idx;
}
static void dijkstra(int[][] arr, int v){
for(int i=0; i<n; i++)
distance[i] = arr[v][i];
visit[v] = true; //시작 정점 방문
for(int i=0; i<n-2; i++){
int current = getMinIdx(); //distance에서 가장 작은 값의 인덱스 반환
visit[current] = true;
for(int j=0; j<n; j++){
if(!visit[j] && distance[current] + arr[current][j] < distance[j])
distance[j] = distance[current] + arr[current][j];
}
}
}
public static void main(String[] args) {
int[][] arr = {
{0, 7, 9, INF, INF, 14},
{7, 0, 10, 15, INF, INF},
{9, 10, 0, 11, INF, 2},
{INF, 15, 11, 0, 6, INF},
{INF, INF, INF, 6, 0, 9},
{14, INF, 2, INF, 9, 0}
};
dijkstra(arr, 0);
for(int i=0; i<n; i++)
System.out.print(distance[i] + " ");
}
}다만 위 코드로 실행할 시 정점의 개수의 비해 간선이 현저히 적을 때 엄청 비효율적으로 작동하게 된다. 정점이 10만개이고 간선이 2개라고 해도
//가장 최소 거리를 가지는 정점을 반환
static int getMinIdx(){
int min = INF;
int idx = 0;
for(int i=0; i<n; i++)
if(!visit[i] && distance[i] < min){ //방문하지 않았고, 거리가 가장 짧은 곳의 idx
min = distance[i];
idx = i;
}
return idx;
}이 코드를 통해 10만번 반복을 돌고, 다익스트라 함수에서 10만번 반복을 하기 때문에 O(N*N) 시간 복잡도를 가져가게 된다. 이를 선형 탐색을 이용한 다익스트라 라고 할 수 있다. 백준이나 프로그래머스에서 문제를 풀경우 시간초과를 발생할 확률이 매우 크므로, 힙(Heap)구조를 이용해 O(Nlog N)의 시간 복잡도를 갖는 코드를 구현할 수 있다.
[알고리즘] Dijkstra 알고리즘 - PriorityQueue
[알고리즘] 다익스트라(Dijkstra) 알고리즘 최단 경로 최단 경로 문제에서 입력 그래프의 유형은 크게 두 가지이다. 모든 간선 가중치가 음이 아닌 경우 음의 가중치가 존재하는 경우 음의 가중치
dev-gorany.tistory.com
# 복습 문제
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
1261번: 알고스팟
첫째 줄에 미로의 크기를 나타내는 가로 크기 M, 세로 크기 N (1 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 미로의 상태를 나타내는 숫자 0과 1이 주어진다. 0은 빈 방을 의미하고, 1은 벽을 의미
www.acmicpc.net
# References
쉽게 배우는 알고리즘 개정판. 문병로. 한빛아카데미
C언어로 쉽게 풀어쓴 자료구조 개정3판. 천인국. 생능출판
'Programming > 알고리즘' 카테고리의 다른 글
| [알고리즘] 비트 마스킹(Bit Masking) (0) | 2021.02.21 |
|---|---|
| [알고리즘] Dijkstra 알고리즘 - PriorityQueue (0) | 2021.01.28 |
| [알고리즘] 크루스칼(Kruskal) 알고리즘 (0) | 2021.01.28 |
| [알고리즘] 선택 / 버블 / 삽입 정렬 (0) | 2021.01.26 |
| [알고리즘] 너비 우선 탐색(Breadth-First Search, BFS) (0) | 2021.01.20 |




