- Today
- Total
개발하는 고라니
[알고리즘] Greedy 알고리즘 본문
# 학 습 목 표
- 그리디 알고리즘의 특징을 파악한다.
- 그리디 알고리즘으로 최적해가 보장되는 예와 그렇지 않은 예를 관찰한다.
# 그리디 알고리즘
- 눈 앞의 이익만 취하고 보는 알고리즘
- 현재 시점에 가장 이득이 되어 보이는 해를 선택하는 행위를 반복한다.
- 대부분 최적해와의 거리가 멀다.
- 드물게 최적해가 보장되는 경우도 있다. (최소 신장 트리, 최단 경로 등)do
do {
우선 가장 좋아 보이는 선택을 한다
} until (해 구성 완료)
# 그리디 알고리즘의 전형적 구조
Greedy(C)
C : 원소들의 총 집합
{
S <- ø;
while(C != ø and S는 아직 온전한 해가 아님) {
x <- C에서 가장 좋아 보이는 원소;
집합 C에서 x제거; //C <- C-{x}
if(S에 x를 더해도 됨) then S <- S ∪ {X};
}
if(S가 온전한 해임) then return S;
else return "no solution";
}
/* 최소 신장트리 문제는 이런 방식으로 최적해가 보장되는 드문 예 중 하나이다. */
# 그리디 알고리즘으로 최적해가 보장되지 않는 예
* 이진트리의 최적합 경로 찾기

- 이진트리의 노드의 합이 최대가 되게 찾는다고 할 때, Greedy하게 찾으면 root노드인 10에서 15와 60을 보고 60으로 가는 것으로 결정하게 될 것이다. 결과적으로 72(10+60+2)를 반환 하게된다. 하지만 실제로 최대의 단말노드 까지의 합은 빨간색 화살표로 이어진 경로이다.
* 보따리(Knapsack) 문제 혹은 배낭 문제
- 용량을 초과하지 않는 한 단위 부피당 가치가 가장 큰 물건 순서로 각 물건을 보따리에 추가한다.
- 최적해를 보장하지 못하는 0/1 Knapsack Problem
- (Fractional Knapsack Problem은 최적해를 보장)
* 특정 금액을 만들어야 할 때 가장 적은 동전 갯수의 조합 만들기 문제

- 500원 짜리로 쓸 수 있는 만큼 쓰고 -> 100원 짜리 -> 50원 짜리 -> 10원 짜리 -> 5원 짜리 -> 1원 짜리
- 이렇게 동전의 액면이 모두 바로 아래 액면의 배수가 되면 그리디 알고리즘으로 최적해가 보장 된다.
But, 액면이 바로 아래의 액면의 배수가 되지 않으면 그리디 알고리즘으로 최적해가 보장되지 않는다.
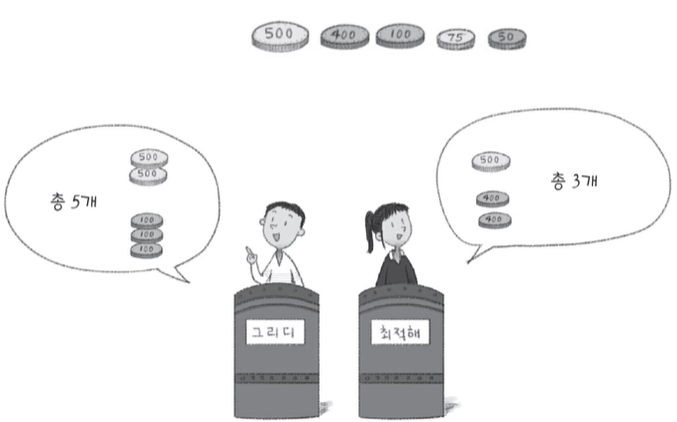
- 위 그림과 같은 상황이면 그리디 알고리즘으로 최적해를 구할 수 없다.
# 그리디 알고리즘으로 최적해를 보장하는 예
* 최소 신장 트리 찾기를 위한 Prim 알고리즘과 Kruskal 알고리즘
Prim(G, r)
{
S <- ø;
정점 r을 방문되었다고 표시하고, 집합 S에 포함시킨다;
while(S != V) {
S에서 V-S를 연결하는 간선들 중 최소길이의 간선(x, y)를 찾는다;
정점 y를 방문되었다고 표시하고, 집합 S에 포함시킨다;
}
}
* 회의실 배정 문제
- 회의실 1개
- 여러 부서에서 회의실 사용 요청 (회의 시작 시간과 종료 시간을 명시해서 신청)
- Greedy한 ideas
- 소요 시간이 가장 짧은 회의순 배정
- 시작 시간이 가장 이른 회의순 배정
- 종료 시간이 가장 이른 회의순 배정 <-- 이것 만이 최적해를 보장
* 그 밖의 예...
- 최단 경로를 구하는 다익스트라 알고리즘
- 허프만 코딩 알고리즘
'Programming > 알고리즘' 카테고리의 다른 글
| [알고리즘] 크루스칼(Kruskal) 알고리즘 (0) | 2021.01.28 |
|---|---|
| [알고리즘] 선택 / 버블 / 삽입 정렬 (0) | 2021.01.26 |
| [알고리즘] 너비 우선 탐색(Breadth-First Search, BFS) (0) | 2021.01.20 |
| [알고리즘] 깊이 우선 탐색(Depth-First Search, DFS) (0) | 2021.01.20 |
| [알고리즘] 동적 프로그래밍 (DP, Dynamic Programming) (0) | 2020.12.07 |




